10 Channel Coding and Interleaving
Требуемые условия завершения
10.2 Block Codes Examples
Example: Error detection using parity check
The parity bit is a binary control symbol, chosen in a way that the resulting binary code word contains an even number of ones (even parity) (alternatively an odd number of ones (odd parity)). The rule for formation of the parity bit can be written using the XOR (\( \otimes \)) function.
A code using one additional parity bit has the distance d = 2, i.e. this code can detect all code words with
e = d – 1 = 2 – 1 = 1
one erroneous symbol e. An error correction is not possible
Example: Error correction with Hamming code
A Hamming code is based on the simple realization of parity bits. But for this code multiple partial parity bits are used. This results in a larger distance d and allows the correction of errors. The partial parity bits are built for a well-defined number of message symbols.

Figure 10-8: Graphical demonstration of a Hamming code.
The example of the Hamming code in Figure 10-8 consists of four message symbols and three control symbols. The control symbols are derived as the parity bit of that circle in which the control symbol is included.
The resulting code ensures that any two message words that only differ in one symbol have at least two different control symbols so that the distance of the code is d = 3. The code can detect
e = d – 1 = 3 – 1 = 2
two erroneous symbols and
t = (d - 1)/2 = (3 - 1)/2 = 1
correct one erroneous symbol.
For erroneous transmission also here the control symbols calculated at the receiver differ from the received ones. The kind of difference shows which code symbol has been falsified during transmission.
The building rules are: z1 = x1 \( \otimes \) x2 \( \otimes \) x3; z2 = x1 \( \otimes \) x2 \( \otimes \) x4; z3 = x1 \( \otimes \) x3 \( \otimes \) x4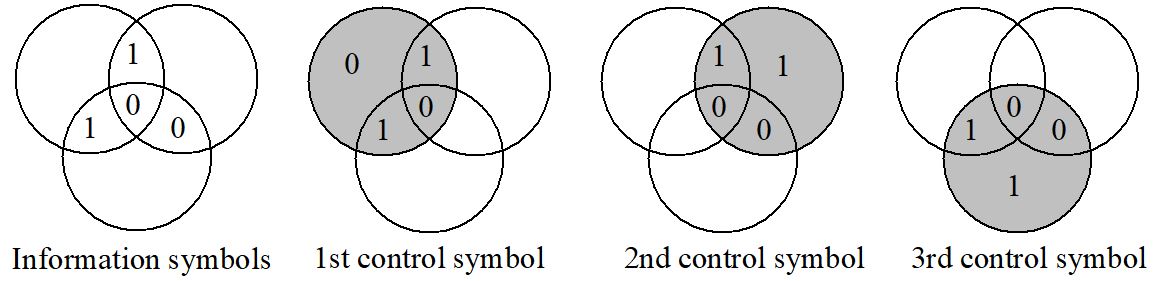
If the first code symbol x1 is falsified all three control symbols calculated at the receiver differ from those calculated in the transmitter, because x1 is contained in all three control equations. The complete check is given in Tab. 10-3. In the first column the place of the error is given, the other columns give the results of the comparison of (correctly) received and calculated control symbol. From Tab. 10-3 we can see that it is possible to determine which code symbol is falsified. Furthermore, we see that with three control symbols 2³ - 1 = 7 different error patterns can be corrected. With k control symbols 2k - 1 different error patterns can be corrected.
The parity bit is a binary control symbol, chosen in a way that the resulting binary code word contains an even number of ones (even parity) (alternatively an odd number of ones (odd parity)). The rule for formation of the parity bit can be written using the XOR (\( \otimes \)) function.
A code using one additional parity bit has the distance d = 2, i.e. this code can detect all code words with
e = d – 1 = 2 – 1 = 1
one erroneous symbol e. An error correction is not possible
t = (d/2) - 1 = (2/2) - 1 = 0.
Tab.
10-1
| transmitted code word |
transmitted parity bit p |
received code word |
received parity bit p' |
parity bit built in the receiver \( \tilde{p}' \) |
result of comparison |
error detection |
|---|---|---|---|---|---|---|
| 0110100 | 1 | 0110101 | 1 | 0 |
\( p' \neq \tilde{p}' \) | yes |
| 0110100 | 1 | 0100100 | 1 | 0 |
\( p' \neq \tilde{p}' \) | yes |
| 0110100 | 1 | 0100101 | 1 | 1 |
\( p' = \tilde{p}' \) | no |
| 0110100 | 1 | 0110100 | 0 | 1 |
\( p' \neq \tilde{p}' \) | yes, but only parity bit falsified |
A Hamming code is based on the simple realization of parity bits. But for this code multiple partial parity bits are used. This results in a larger distance d and allows the correction of errors. The partial parity bits are built for a well-defined number of message symbols.
Figure 10-8: Graphical demonstration of a Hamming code.
The example of the Hamming code in Figure 10-8 consists of four message symbols and three control symbols. The control symbols are derived as the parity bit of that circle in which the control symbol is included.
The resulting code ensures that any two message words that only differ in one symbol have at least two different control symbols so that the distance of the code is d = 3. The code can detect
e = d – 1 = 3 – 1 = 2
two erroneous symbols and
t = (d - 1)/2 = (3 - 1)/2 = 1
correct one erroneous symbol.
For erroneous transmission also here the control symbols calculated at the receiver differ from the received ones. The kind of difference shows which code symbol has been falsified during transmission.
The building rules are: z1 = x1 \( \otimes \) x2 \( \otimes \) x3; z2 = x1 \( \otimes \) x2 \( \otimes \) x4; z3 = x1 \( \otimes \) x3 \( \otimes \) x4
Figure
10-9:
Building rules.
Tab.
10-2
Check:| message symbols x1 x2 x3 x4 |
control symbols z1 z2 z3 |
|---|---|
| 0 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 0 1 0 1 0 1 1 0 0 1 1 1 1 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1 |
0 0 0 0 1 1 1 0 1 1 1 0 1 1 0 1 0 1 0 1 1 0 0 0 1 1 1 1 0 0 0 1 0 0 0 1 0 0 1 0 1 0 1 0 0 1 1 1 |
If the first code symbol x1 is falsified all three control symbols calculated at the receiver differ from those calculated in the transmitter, because x1 is contained in all three control equations. The complete check is given in Tab. 10-3. In the first column the place of the error is given, the other columns give the results of the comparison of (correctly) received and calculated control symbol. From Tab. 10-3 we can see that it is possible to determine which code symbol is falsified. Furthermore, we see that with three control symbols 2³ - 1 = 7 different error patterns can be corrected. With k control symbols 2k - 1 different error patterns can be corrected.
Tab.
10-3
| Erroneous code symbol |
comparison control symbol 1 \( z'_1 = \tilde{z}'_1 \) |
comparison control symbol 2 \( z'_2 = \tilde{z}'_2 \) |
comparison control symbol 3 \( z'_3 = \tilde{z}'_3 \) |
|---|---|---|---|
| \( x'_1 \neq x_1 \) | no | no | no |
| \( x'_2 \neq x_2 \) | no | no | yes |
| \( x'_3 \neq x_3 \) |
no | yes | no |
| \( x'_4 \neq x_4 \) |
yes | no | no |
| \( z'_1 \neq z_1 \) | no | yes | yes |
| \( z'_2 \neq z_2 \) |
yes | no | yes |
| \( z'_3 \neq z_3 \) |
yes | yes | no |