10 Channel Coding and Interleaving
Completion requirements
10.1 Fundamentals of Coding Theory
For channel coding the redundancy of the
message is increased intentionally to allow detection and correction of errors.
A message is a compilation of symbols or states used for transmission of information.
An alphabet A denotes the symbol set consisting of a defined list of symbols or symbol types. The number of symbols of an alphabet is called its size or symbol range sr. A word is a composition of n symbols to a unit. In communication theory theses word most of the time consist of the symbols 0 and 1 (A = {0,1}, sr = 2), but also the 26 letters of the German alphabet are symbols that can be composed to words of the German language. The number n of symbols of a value is called word length. The composition of single words from symbols has to be defined because not every random combination of symbols is or shall be defined as a word.
A Code is an assignment rule between two sets of words. Code words are these words that can be composed from code symbols and that are assigned to a source word. Only if words exist that are not defined as code word errors can be detected.
With channel coding the words of the message source are coded in a way that codes result which should still differ even if single code symbols are falsified. For such code words the receiver has the possibility to detect errors added during transmission. If the code is chosen accordingly the receiver even can correct errors. In turn the insertion of redundancy in the message has to be accepted.
For assessment of the detection and correction capabilities of a code we need to know in how many symbols the code words of the code differ from each other. The weight of a binary code is the number of ones in the code. The Hamming distance h is the number of code symbols in which two code words of the same length differ if corresponding places in the words are compared:
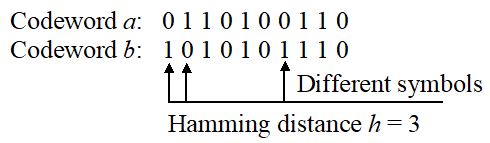
Figure 10-3: Hamming distance of two code words.
The distance d of a code is the smallest of all Hamming distances of any two different code words
\( d=min\{h\} \), (10-1)
i.e. any two chosen code words always differ in at least d symbols.
For transmission at minimum d code symbols have to be falsified to turn a transmitted code word into another code word. If less than d code symbols are falsified the receiver detects the error because it does not receive a code word.
A symbol that is converted into another symbol during the transmission is called erroneous symbol and a word that is not a code word is called erroneous word (word containing erroneous symbols).
A code with distance d allows the receiver to detect these words as erroneous that contain d – 1 or less erroneous symbols. The number of erroneous symbols that can be detected at least is
\( e=d-1 \). (10-2)
If we assume that the probability of one erroneous symbol is higher than that of two erroneous symbols and that is higher than the probability of three erroneous symbols and so on, then we have the possibility to correct errors. The correction can be done assigning the erroneous received words to those code words from which they are falsified with highest probability.
A code with odd distance d can correct all erroneous words containing no more than
\( t = \frac{d-1}{2} \) (10-3)
erroneous code symbols. t denotes the minimum number of erroneous code symbols that can be corrected. In Figure 10-4 the assignment of the erroneous words to the code words is shown. An assignment is possible as long as an erroneous word has a smaller distance to one code word CWi compared to all other code words CWj.
A code with even distance d can correct all erroneous words containing no more than
\( t= \frac{d}{2}-1 \) (10-4)
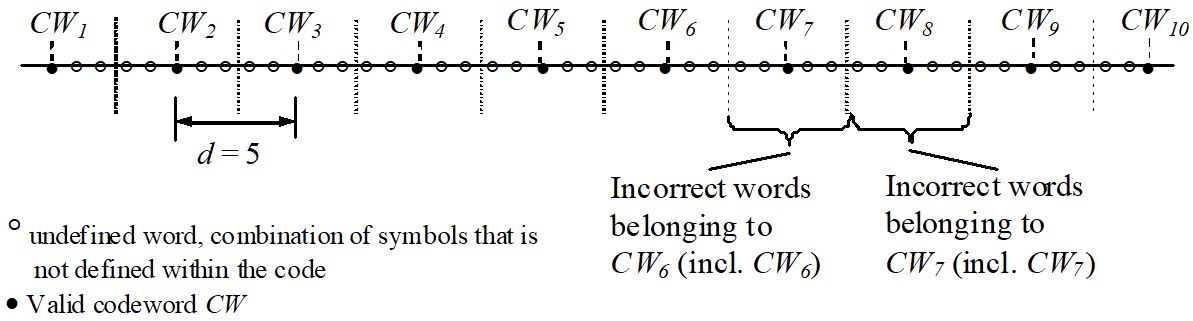
Figure 10-4: Assignment of erroneous words to code words for odd distance d.
A message is a compilation of symbols or states used for transmission of information.
An alphabet A denotes the symbol set consisting of a defined list of symbols or symbol types. The number of symbols of an alphabet is called its size or symbol range sr. A word is a composition of n symbols to a unit. In communication theory theses word most of the time consist of the symbols 0 and 1 (A = {0,1}, sr = 2), but also the 26 letters of the German alphabet are symbols that can be composed to words of the German language. The number n of symbols of a value is called word length. The composition of single words from symbols has to be defined because not every random combination of symbols is or shall be defined as a word.
A Code is an assignment rule between two sets of words. Code words are these words that can be composed from code symbols and that are assigned to a source word. Only if words exist that are not defined as code word errors can be detected.
With channel coding the words of the message source are coded in a way that codes result which should still differ even if single code symbols are falsified. For such code words the receiver has the possibility to detect errors added during transmission. If the code is chosen accordingly the receiver even can correct errors. In turn the insertion of redundancy in the message has to be accepted.
For assessment of the detection and correction capabilities of a code we need to know in how many symbols the code words of the code differ from each other. The weight of a binary code is the number of ones in the code. The Hamming distance h is the number of code symbols in which two code words of the same length differ if corresponding places in the words are compared:
Figure 10-3: Hamming distance of two code words.
The distance d of a code is the smallest of all Hamming distances of any two different code words
\( d=min\{h\} \), (10-1)
i.e. any two chosen code words always differ in at least d symbols.
For transmission at minimum d code symbols have to be falsified to turn a transmitted code word into another code word. If less than d code symbols are falsified the receiver detects the error because it does not receive a code word.
A symbol that is converted into another symbol during the transmission is called erroneous symbol and a word that is not a code word is called erroneous word (word containing erroneous symbols).
A code with distance d allows the receiver to detect these words as erroneous that contain d – 1 or less erroneous symbols. The number of erroneous symbols that can be detected at least is
\( e=d-1 \). (10-2)
If we assume that the probability of one erroneous symbol is higher than that of two erroneous symbols and that is higher than the probability of three erroneous symbols and so on, then we have the possibility to correct errors. The correction can be done assigning the erroneous received words to those code words from which they are falsified with highest probability.
A code with odd distance d can correct all erroneous words containing no more than
\( t = \frac{d-1}{2} \) (10-3)
erroneous code symbols. t denotes the minimum number of erroneous code symbols that can be corrected. In Figure 10-4 the assignment of the erroneous words to the code words is shown. An assignment is possible as long as an erroneous word has a smaller distance to one code word CWi compared to all other code words CWj.
A code with even distance d can correct all erroneous words containing no more than
\( t= \frac{d}{2}-1 \) (10-4)
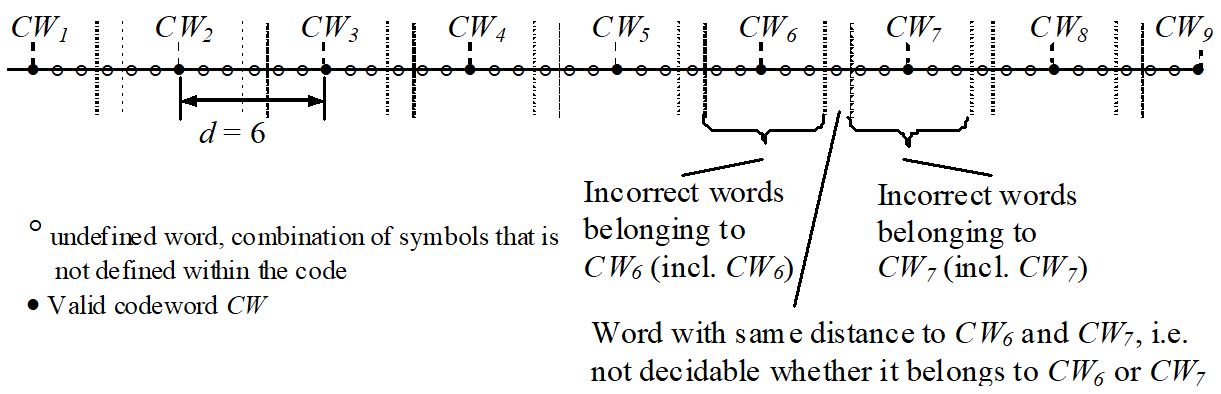
erroneous code symbols. This is because a word
with same distance to two code words cannot be assigned unambiguously.
Figure 10-4: Assignment of erroneous words to code words for odd distance d.
Figure 10-5: Assignment of erroneous words to code words for even distance d.